Свойства вписанной в треугольник окружности

В этой статье Вы сможете найти свойства вписанной в треугольник окружности, а также их доказательства.

Вписанная в треугольник окружность - это такая окружность, которая находится внутри треугольника и при этом касается всех его сторон (то есть все стороны треугольника являются касательными к окружности). Стоит отметить, что в этом случае сам треугольник является описанным вокруг данной окружности.

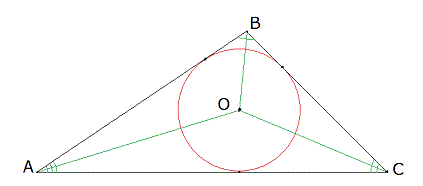
Рисунок 1

Свойства вписанной в треугольник окружности

1. Центр вписанной в треугольник окружности (на рис. 1 – точка О) лежит на пересечении биссектрис треугольника (на рис.1 – АО, ВО и СО).
2. В любой треугольник вписывается окружность и притом только одна.
3. Радиус вписанной в треугольник окружности равен:

   

   
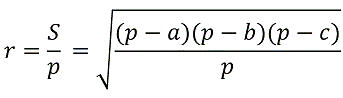
   Где S – это площадь треугольника,
   p - полупериметр треугольника,
   a, b, c - стороны треугольника.

Доказательства свойств

Первое свойство

Доказать, что центр вписанной в треугольник окружности находится на пересечении биссектрис.

Доказательство.

1. Опустим из центра окружности перпендикуляры (OL, OK и OM) к каждой из сторон треугольника ABC (рис. 2). Также из каждого угла проведем прямую к центру окружности (OA, OC и OB).

   

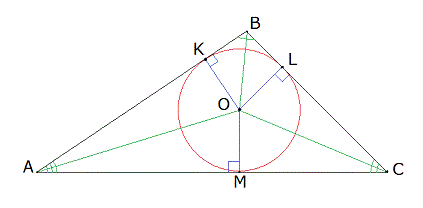
   Рисунок 2

2. Рассмотрим 2 треугольника AOM и AOK. Они являются прямоугольными, т.к. OM и OK – перпендикуляры к сторонам AC и AB. Гипотенуза OA является общей для обоих треугольников.
3. Поскольку касательная к окружности перпендикулярна радиусу, проведенному в точку касания (свойство касательной к окружности), то катеты OМ и OК являются радиусами окружности и, следовательно, равны.
4. Из вышесказанного следует, что прямоугольные треугольники AOМ и AOК равны по гипотенузе и катету. Т.к. треугольники равны, то углы OAМ и OAК тоже равны, отсюда следует, что OA – биссектриса угла BAC.
5. Аналогичным образом доказывается, что OC – биссектриса угла ACB, а OB – биссектриса угла ABC.
6. То есть биссектрисы треугольника пересекаются в одной точке и этой точкой является центр вписанной окружности.

Что и требовалось доказать.

Второе свойство

Доказать, что в любой треугольник можно вписать окружность и притом только одну.

Доказательство

1. В треугольник можно вписать окружность только в том случае, если найдется точка равноудаленная от его сторон.
2. Проведем 2 биссектрисы OA и OC. Опустим из точки их пресечения перпендикуляры (OK, OL и OM) ко всем трем сторонам треугольника ABC (рис. 3).

   

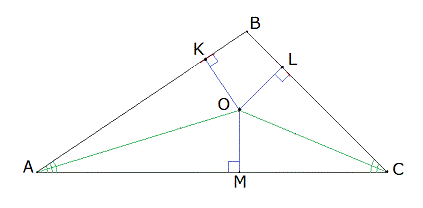
   Рисунок 3

3. Рассмотрим треугольники AOK и AOM.
4. У них общая гипотенуза AO. Углы OAK и OAM равны (т.к. OA – биссектриса угла KAM). Углы OKA и OMA прямые (т.е. тоже равны), т.к. OK и OM – перпендикуляры к сторонам AB и AC соответственно.
5. Поскольку 2 пары углов равны, то и 3-я пара (AOM и AOK) также является равной.
6. Из вышенаписанного следует, что треугольники AOK и AOM равны по стороне (AO) и 2-м прилежащим к ней углам (рис. 4).

   

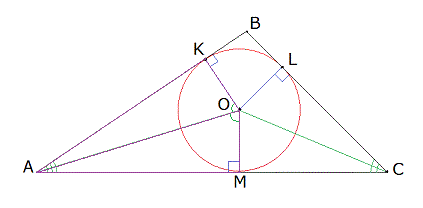
   Рисунок 4

7. Отсюда следует, что стороны OM и OK равны, т.е. равноудалены от сторон треугольника AC и AB соответственно.
8. Аналогичным образом доказывается, что OM и OL равны, т.е. они равноудалены от сторон треугольника AC и BC соответственно.
9. Из вышенаписанного следует, что точка O равноудалена от сторон треугольника, т.е. является центром вписанной окружности.
10. Аналогичным образом можно найти точку внутри любого треугольника, которая будет равноудалена от его сторон, то есть будет центром вписанной в этот треугольник окружности.
11. Из вышенаписанного следует, что в любой треугольник можно вписать окружность.
12. Следует отметить, что центр данной окружности лежит на пересечении биссектрис треугольника.
13. Допустим, что в треугольник можно вписать две (или более) окружности.
14. Проведя 3 отрезка из вершин треугольника к центру этой окружности и, опустив перпендикуляры из этого центра к каждой из сторон треугольника, мы сможем доказать, что эта окружность лежит на пересечении биссектрис треугольника (см. доказательство первого свойства).
15. То есть центр этой окружности совпадает с центром первой окружности, уже вписанной в треугольник, а ее радиус равен перпендикуляру, опущенному на сторону треугольника (как и в первом случае). Это говорит о том, что данные окружности совпадают.
16. Аналогичным образом можно доказать, что любая новая вписанная окружность совпадает с первой, которую мы впишем.
17. То есть вписать в треугольник можно только одну окружность.

Что и требовалось доказать.

Третье свойство

Доказать, что радиус вписанной окружности r равен отношению площади треугольника S к полупериметру p.

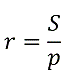
А также равенство:

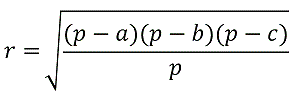
Доказательство.

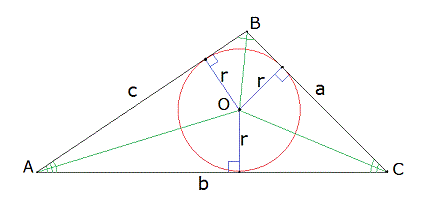
Рисунок 5

1. Рассмотрим произвольный треугольник ABC со сторонами a, b и c (рис 5). Полупериметр данного треугольника p рассчитывается по формуле:

   

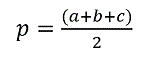
2. Центр нашей окружности (точка O на рис. 5) находиться на пересечении биссектрис треугольника. Отрезки OA, OB и OC, соединяющие O с вершинами треугольника АВС, делят треугольник на три: AOC, COB, BOA. Площадь треугольника ABC можно найти как сумму площадей этих трех треугольников.

   

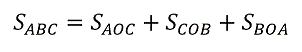
3. Поскольку площадь любого треугольника равна половине произведения его основания на высоту, а высота треугольников AOC, COB, BOA равна радиусу окружности r, то площади треугольников AOC, COB и BOA можно найти как:

   

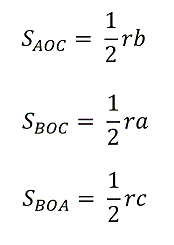
4. Выразим площадь S треугольника ABC через сумму площадей этих трех треугольников:

   

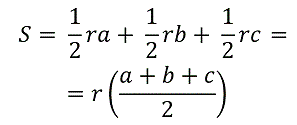
5. Заметив, что второй множитель – это полупериметр треугольника ABC, можно представить наше равенство в виде:

   

   Или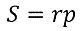

   

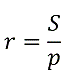
6. Итак, мы доказали, что радиус вписанной окружности равен отношению площади треугольника к полупериметру.
7. Вспомним формулу Герона, которая в нашем случае будет иметь вид:

   

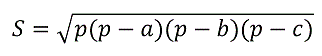
8. Теперь радиус можно выразить как:

   

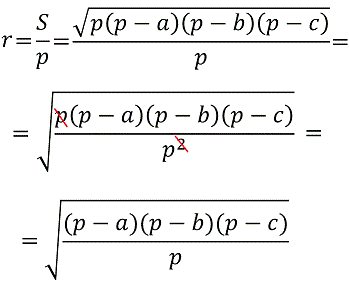
Что и требовалось доказать.

Понравилась статья, расскажите о ней друзьям: